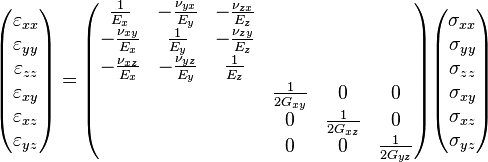robert hooke fue uncientífico inglés. Es considerado uno de los científicos experimentales más importantes de la historia de la ciencia, polemista incansable con un genio creativo de primer orden. Sus intereses abarcaron campos tan dispares como la biología, la medicina, la horología (cronometría), la físicaplanetaria, la mecánica de sólidos deformables, la microscopía, la náutica y la arquitectura. Participó en la creación de la primera sociedad científica de la historia, la Royal Society de Londres. Sus polémicas con Newton acerca de la paternidad de la ley de la gravitación universal han pasado a formar parte de la historia de la ciencia:1 parece ser que Hooke era muy prolífico en ideas originales que luego rara vez desarrollaba.
Asumió en 1662 el cargo de director de experimentación en la Sociedad Real de Londres,1 de la cual llegó a ser también secretario en 1677. Pese al prestigio que alcanzó en el ámbito de la ciencia, sus restos yacen en una tumba desconocida, en algún punto del norte de Londres. En los últimos años, algunos historiadores y científicos han puesto gran empeño en reivindicar a este “genio olvidado”, por usar las palabras de uno de sus biógrafos, Stephen Inwood. En el año 2003, al cumplirse el tercer centenario de la muerte de Hooke, el Real Observatorio de Greenwich(situado en Londres) exhibió algunos de sus extraordinarios inventos y hallazgos.
ley de la estacidad de hooke
En 1660, mientras trabajaba como ayudante de Robert Boyle, formuló lo que hoy se denomina ley de elasticidad de Hooke,1 que describe cómo un cuerpo elástico se estira de forma proporcional a la fuerza que se ejerce sobre él, lo que dio lugar a la invención del resorte helicoidal o muelle.
En 1665 publicó el libro Micrographía, el relato de 50 observaciones microscópicas y telescópicas con detallados dibujos. Este libro contiene por primera vez la palabracélula y en él se apunta una explicación plausible acerca de los fósiles.
Hooke descubrió las células observando en el microscopio una lámina de corcho, dándose cuenta de que estaba formada por pequeñas cavidades poliédricas que recordaban a las celdillas de un panal. Por ello cada cavidad se llamó célula. No supo demostrar lo que estas celdillas significaban como constituyentes de los seres vivos. Lo que estaba observando eran células vegetales muertas con su característica forma poligonal.
Durante cuarenta años fue miembro, secretario y bibliotecario de la Royal Society de Londres y tenía la obligación de presentar ante la sociedad un experimento semanal.
Además de las observaciones publicadas en Micrographía y de la formulación de la ley de elasticidad de Hooke, Hooke formuló la teoría del movimiento planetario como un problema de mecánica, y mantuvo continuas disputas con su contemporáneoIsaac Newton respecto a la teoría de la luz y la ley de la gravitación universal. En 1672 intentó comprobar que la Tierra se mueve en un elipse alrededor del Sol y seis años más tarde propuso la ley inversa del cuadrado.
Hooke alegaba haber descubierto él la ley de la gravitación (entendida como la ley inversa del cuadrado. Sí que está documentada su propuesta como una atracción atenuada de forma no especificada con la distancia), pero nunca se mostró a la luz pública documentos que lo respaldaran. En varias ocasiones pidió que se celebrara un juicio sobre el asunto, que nunca llegó. Existieron rumores de un supuesto plagio realizado por Newton, puesto que pudo haber visitado el estudio de Hooke, estando éste ausente, pudiendo, así, haber revisado documentos y escritos de Hooke. Esto podría explicar el por qué Hooke reclamó incesantemente la celebración del juicio. No se han encontrado pruebas del supuesto plagio. También mantuvo una durísima polémica, que duraría decenios, referida a la teoría de la luz, la cual Hooke afirmaba haber descrito en su Micrographia.
ley de la elasticidad consiste en :
La ley de elasticidad de Hooke o ley de Hooke, establece la relación entre el alargamiento o estiramiento longitudinal y la fuerza aplicada. La elasticidad es la propiedad física en la que los objetos con capaces de cambiar de forma cuando actúa una fuerza de deformación sobre un objeto. El objeto tiene la capacidad de regresar a su forma original cuado cesa la deformación. Depende del tipo de material. Los materiales pueden ser elásticos o inelásticos. Los materiales inelásticos no regresan a su forma natural.
La forma más común de representar matemáticamente la Ley de Hooke es mediante la ecuación del muelle o resorte, donde se relaciona la fuerza  ejercida por el resorte con la elongación o alargamiento
ejercida por el resorte con la elongación o alargamiento  provocado por la fuerza externa aplicada al extremo del mismo:
provocado por la fuerza externa aplicada al extremo del mismo:
 ejercida por el resorte con la elongación o alargamiento
ejercida por el resorte con la elongación o alargamiento  provocado por la fuerza externa aplicada al extremo del mismo:
provocado por la fuerza externa aplicada al extremo del mismo:
donde  se llama constante elástica del resorte y
se llama constante elástica del resorte y  es su elongación o variación que experimenta su longitud.
es su elongación o variación que experimenta su longitud.
 se llama constante elástica del resorte y
se llama constante elástica del resorte y  es su elongación o variación que experimenta su longitud.
es su elongación o variación que experimenta su longitud.
La energía de deformación o energía potencial elástica  asociada al estiramiento del resorte viene dada por la siguiente ecuación:
asociada al estiramiento del resorte viene dada por la siguiente ecuación:
 asociada al estiramiento del resorte viene dada por la siguiente ecuación:
asociada al estiramiento del resorte viene dada por la siguiente ecuación:
Es importante notar que la  antes definida depende de la longitud del muelle y de su constitución. Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando
antes definida depende de la longitud del muelle y de su constitución. Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando  por la longitud total, y llamando al producto
por la longitud total, y llamando al producto 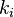 o
o  intrínseca, se tiene:
intrínseca, se tiene:
 antes definida depende de la longitud del muelle y de su constitución. Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando
antes definida depende de la longitud del muelle y de su constitución. Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando  por la longitud total, y llamando al producto
por la longitud total, y llamando al producto 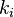 o
o  intrínseca, se tiene:
intrínseca, se tiene:
Llamaremos  a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas,
a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas,  a la constante de un pequeño trozo de muelle de longitud
a la constante de un pequeño trozo de muelle de longitud  a la misma distancia y
a la misma distancia y  al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza
al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza  . Por la ley del muelle completo:
. Por la ley del muelle completo:
 a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas,
a la tensión en una sección del muelle situada una distancia x de uno de sus extremos que tomamos como origen de coordenadas,  a la constante de un pequeño trozo de muelle de longitud
a la constante de un pequeño trozo de muelle de longitud  a la misma distancia y
a la misma distancia y  al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza
al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza  . Por la ley del muelle completo:
. Por la ley del muelle completo:
Tomando el límite:
que por el principio de superposición resulta:
El comportamiento elástico de un material ortotrópico queda caracterizado por nueve constantes independientes: 3 módulos de elasticidad longitudinal
 , 3 módulos de rigidez
, 3 módulos de rigidez  y 3 coeficientes de Poisson
y 3 coeficientes de Poisson  . De hecho para un material ortotrópico la relación entre las componentes del tensor tensión y las componentes del tensor deformación viene dada por:
. De hecho para un material ortotrópico la relación entre las componentes del tensor tensión y las componentes del tensor deformación viene dada por:Donde:

Como puede verse las componentes que gobiernan el alargamiento y las que gobiernan la distorsión están desacopladas, lo cual significa que en general es posible producir alargamientos en torno a un punto sin provocar distorsiones y viceversa. Las ecuaciones inversas que dan las deformaciones en función de las tensiones toman una forma algo más complicada:
Donde:


resorte :
pequeño video donde explican la ley de la elasticidad: